概要 

近年, マイクロマウスで流行っている軌道追従について自分が行っているKanayama Control Method をもとにした制御の話をしていきます.

はじめに 

この記事ではこの半年, 論文を読んで自分なりに試行錯誤して実装した話を書いています.
タイトルには独立2輪車型のロボットと書いてありますが, 実装は私が作っているマイクロマウスで行っています.
実装するモチベとしては, 「ロボットを複雑な軌道に対しても追従できるようにしたい」, 「再現性のある動きをさせたい」, 「マイクロマウスに出てくる壁が無くても走れるようにしたい」 といった感じで, 「めっちゃ速く走りたい」 といったものではないのでご注意.

本文 

前提 

まずは制御対象を以下のように扱います.

ControlTarget

ロボットの状態は絶対座標での位置と姿勢を表していて, $V$はロボットの並進速度, $w$はロボットの角速度になります.

ここでは入力として$V,w$を与えています. ここで, $V,w$ と $x, y, \theta$の間では以下の関係が成り立っています.
\begin{eqnarray}
\begin{array}{ c }
\dot{x} =V\cos\theta \\\
\dot{y\ } =V\sin\theta \\\
\dot{\theta } =w
\end{array}\
\end{eqnarray}
今回の目標は目標軌道にロボットを追従させることです.
軌道と経路の違いや, 軌道に追従させるとは何かという話はidさんやTokoroさんがこちらのブログで説明しているので, そちらを見てくれると分かりやすいと思います.
独立二輪車型ロボットで目標軌道に追従する制御をする①
軌道と経路の違い | Tokoro’s Tech-Note

実装はこちらの論文を読んで行いました.

A stable tracking control method for an autonomous mobile robot

こちらの論文をざっくりと読むと, 軌道とのズレをコントローラーの入力にフィードバックすることで, 目標とする軌道との誤差が0に漸近収束するという内容です.(正直これは私が説明するよりも読んでみたほうが理解がしやすいと思います)
自分の現在位置を$P_c$, 目標の点を$P_r$, そして誤差を$P_e$とした際に, 以下の関係が成り立ちます.
\begin{equation}
P_{e} =\ \begin{bmatrix}
x_{e}\\\
y_{e}\\\
\theta _{e}
\end{bmatrix} =\begin{bmatrix}
\cos \theta _{c} & \sin \theta _{c} & 0\\\
-\sin \theta {c} & \cos \theta {c} & 0\\\
0 & 0 & 1
\end{bmatrix}( P{r} -P{c})
\end{equation}

図に表すとこんな感じです. (こちらは論文の図を参考に描いております)
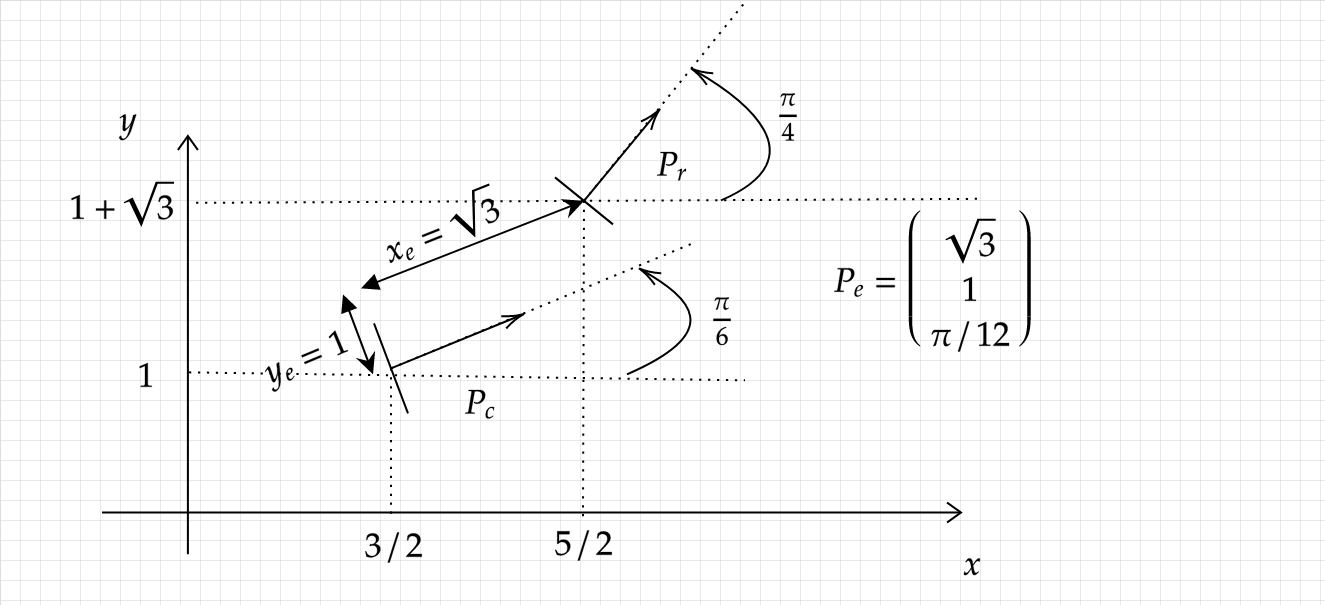
errorPic
そして, コントロールへの入力は以下のようになります.
ここでは$V_r$を目標並進速度, $w_r$を目標角速度としています.
\begin{equation}
\left(\begin{array}{ c }
v\\\
w
\end{array}\right) =\left(\begin{array}{ c }
V_{r}\cos \theta {e} +K{x} x_{e}\\\
w_{r} +V_{r}( K_{y} y_{e} +K_{\theta }\sin \theta _{e})
\end{array}\right)
\end{equation}
ここで,

  • $x_{e} ,\ y_{e} ,\ \theta _{e} $: ロボット座標系から見た目標点に対する誤差
  • $V_{r} ,\ w_{r} $: 目標並進速度, 角速度
  • $K_{x} ,\ K_{y} ,\ K_{\theta } $:パラメータ

となります.

さて, ここまでで軌道追従に必要なものは出揃いました.
ここで私達がマイコンの上にプログラムとして落とし込む上で次のことを考えなくてはいけません. すなわち,

  • どのように軌道をロボットに与えるか.
  • 経路上のどこを目標とするか. (軌道を表す点列の中でどれを目標とするか)

といったことを考慮していく必要があります.
これは様々な実装方法があり,

  • 弧長パラメータを使ってオフラインで軌道を生成し, それを追いかける.
  • 予め$V_r,w_r$をある値に設定してシュミレーションを行い, その結果として得られた$x,y,\theta$とともに, 時系列情報として$x,y,\theta , V_r, w_r$を構造体に入れる.

などの実装方法があります. しかし, 前者は近似式を求めるのがめんどくさい, 後者は決められた目標並進速度と角速度でしか走ることができず, 気軽にパラメーター上げができない, といった問題があります.
一長一短のそれぞれの実装方法ですが, 私は最もシンプルな
目標角速度を与えて一定間隔で点列を作り, その点列群の$x,y,\theta$情報をマイコンに構造体でもたせる
という実装方法を行いました.
以下では私の実装方法について書いていきます.

実装 

前段階 

前段階の処理として, 軌道の点列を生成する必要があります.
私はけりさんがブログに上げているMATLABコードを使いました.
MATLABでスラローム軌道生成 KERI’s Lab

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206

clear;
%% 区画の大きさを定義 [mm]
seg_full = 180;
seg_half = seg_full / 2;

%% パターンを選択
% adv_straight: カーブ前の直線部分の長さ [mm]
% pos_start: 始点位置 [x; y; theta]
% pos_start: 終点位置 [x; y; theta]
switch 9
    case 0 % #0 search 90
        adv_straight = 5;
        pos_start = [0; 0; 0];
        pos_end = [seg_half; seg_half; pi/2];
    case 1 % #1 最短 45
        adv_straight = 40;
        pos_start = [0; 0; 0];
        pos_end = [seg_full; seg_half; pi/4];
    case 2 % #2 最短 90
        adv_straight = 50;
        pos_start = [0; 0; 0];
        pos_end = [seg_full; seg_full; pi/2];
    case 3 % #3 最短 135
        adv_straight = 40;
        pos_start = [0; 0; 0];
        pos_end = [seg_half; seg_full; 3/4*pi];
    case 4 % #4 最短 180
        adv_straight = 50;
        pos_start = [0; 0; 0];
        pos_end = [0; seg_full; pi];
    case 5 % #5 最短 斜め 90
        adv_straight = 5;
        pos_start = [0; 0; pi/4];
        pos_end = [0; seg_full; 3/4*pi];
    case 6 % #6 最短 ロング 斜め 90
        adv_straight = 0;
        pos_start = [0; 0; pi/4];
        pos_end = [0; seg_full * 2; 3/4*pi];
    case 7 % #7 最短 ロング 135
        adv_straight = 0;
        pos_start = [0; 0; 0];
        pos_end = [seg_half; seg_full * 2; 3/4*pi];
    case 8 % #8 最短 ロング 180
        adv_straight = 0;
        pos_start = [0; 0; 0];
        pos_end = [seg_half; seg_full * 2; pi];
    case 9 % #9 V90
        adv_straight = 30;
        pos_start = [0; 0; -pi/4];
        pos_end = [seg_full; 0; pi/4];
end

%% 設定情報
% 点列の間隔 [mm]
dx = 1.0;
% 角速度と角加速度を設定
omega_dot = 150 * pi;
omega_max = 5 * pi;

%% 必要情報の算出
% スタートポジションの同時変換行列を生成
Rot_start = [cos(pos_start(3)),-sin(pos_start(3)),0;sin(pos_start(3)),cos(pos_start(3)),0;0,0,1];
% オフセットを消去し目標位置を算出
pos_target = Rot_start \ (pos_end - pos_start) - [adv_straight; 0; 0];
% 正弦波加速の1周期の時間を算出
T = omega_max / omega_dot * pi;
[t, theta] = ode45(@(t, theta) omega_max * sin(pi*t/T)^2, [0 T], 0); %#ok<ASGLU>

%% 積分結果が目標角度を超えているかどうかで条件分岐
if pos_target(3) < theta(end)
    %% 積分結果が目標角度を超えている場合
    % 終点角度が目標角度になるようなスケーリング係数
    theta_gain = sqrt(pos_target(3) / theta(end));
    % 時間をスケーリング
    T = T * theta_gain;
    % 数値積分で軌跡を生成
    [t, x] = ode45(@(t, x) cos(theta_gain * ((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi))), [0 T], 0);
    [t, y] = ode45(@(t, x) sin(theta_gain * ((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi))), [0 T], 0);
    % 終点位置が目標位置になるように並進速度を算出
    syms v;
    v = double(solve((pos_target(2)-v*y(end))*cos(pos_target(3))==(pos_target(1)-v*x(end))*sin(pos_target(3)), v));
    %% 軌道の表示，生成
    dt = dx/v;
    x_end = x(end)*v; y_end = y(end)*v;
    % 角速度の配列を生成
    figure();
    omega = omega_max * sin(pi*[0:dt:T]/T).^2;
    subplot(6, 1, 1); hold off;
    plot(0:dt:T, omega, '.', 'MarkerSize', 12); grid on;
    % 角度の配列を生成
    [t, theta] = ode45(@(t, theta) theta_gain * omega_max * sin(pi*t/T)^2, [0:dt:T], 0);
    subplot(6, 1, 2); hold off;
    plot(t, theta, '.', 'MarkerSize', 12); grid on;
    % 位置の配列を生成
    [t, x] = ode45(@(t, x) v * cos(theta_gain * ((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi))), [0:dt:T], 0);
    [t, y] = ode45(@(t, y) v * sin(theta_gain * ((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi))), [0:dt:T], 0);
    subplot(6, 1, [3 6]); hold off;
    plot(x, y, '.', 'MarkerSize', 12); grid on;
    % 出力データを生成
    pos = [x, y, theta];
    pos = [pos; x_end, y_end, pos_target(3)];
else
    %% 積分結果が目標角度に満たない場合
    % 角速度が一定の時間を設けて目標角度になるように調節する
    % 角速度 加速時間
    T1 = T / 2;
    % 角速度 一定時間
    T2 = T1 + (pos_target(3) - theta(end)) / omega_max;
    % 角速度 減速時間
    T3 = T2 + T / 2;
    % 数値積分で軌跡を生成
    [t, x1] = ode45(@(t, x1) cos((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi)), [0 T/2], 0);
    [t, x2] = ode45(@(t, x2) cos((omega_max*T/2)/2 - (T*omega_max*sin((2*pi*T/2)/T))/(4*pi) + omega_max*(t-T1)), [T1 T2], x1(end));
    [t, x3] = ode45(@(t, x3) cos(omega_max*(T2-T1) + (omega_max*(t-T2+T1))/2 - (T*omega_max*sin((2*pi*(t-T2+T1))/T))/(4*pi)), [T2 T3], x2(end));
    [t, y1] = ode45(@(t, y1) sin((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi)), [0 T/2], 0);
    [t, y2] = ode45(@(t, y2) sin((omega_max*T/2)/2 - (T*omega_max*sin((2*pi*T/2)/T))/(4*pi) + omega_max*(t-T1)), [T1 T2], y1(end));
    [t, y3] = ode45(@(t, y3) sin(omega_max*(T2-T1) + (omega_max*(t-T2+T1))/2 - (T*omega_max*sin((2*pi*(t-T2+T1))/T))/(4*pi)), [T2 T3], y2(end));
    % 終点位置が目標位置になるように並進速度を算出
    syms v;
    v = double(solve((pos_target(2)-v*y3(end))*cos(pos_target(3))==(pos_target(1)-v*x3(end))*sin(pos_target(3)), v));
    %% 軌道の表示，生成
    dt = dx/v;
    t1 = 0:dt:T1;
    t2 = t1(end):dt:T2;
    t3 = t2(end):dt:T3;
    x1_end = x1(end)*v; x2_end = x2(end)*v; x3_end = x3(end)*v;
    y1_end = x1(end)*v; y2_end = y2(end)*v; y3_end = y3(end)*v;
    % 角速度の配列を生成
    figure();
    subplot(6, 1, 1); hold off;
    plot(t1, omega_max * sin(pi*t1/T).^2, '.', 'MarkerSize', 12); grid on; hold on;
    plot(t2, omega_max+t2*0, '.', 'MarkerSize', 12); grid on; hold on;
    plot(t3, omega_max * sin(pi*(t3-T2+T1)/T).^2, '.', 'MarkerSize', 12); grid on; hold on;
    % 角度の配列を生成
    subplot(6, 1, 2); hold off;
    theta1 = (omega_max*t1)/2 - (T*omega_max*sin((2*pi*t1)/T))/(4*pi);
    theta2 = (omega_max*T/2)/2 - (T*omega_max*sin((2*pi*T/2)/T))/(4*pi) + omega_max*(t2-T1);
    theta3 = omega_max*(T2-T1) + (omega_max*(t3-T2+T1))/2 - (T*omega_max*sin((2*pi*(t3-T2+T1))/T))/(4*pi);
    plot(t1, theta1, '.', 'MarkerSize', 12); grid on; hold on;
    plot(t2, theta2, '.', 'MarkerSize', 12); grid on; hold on;
    plot(t3, theta3, '.', 'MarkerSize', 12); grid on; hold on;
    % 位置の配列を生成
    [t, x1] = ode45(@(t, x1) v*cos((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi)), t1, 0);
    [t, x2] = ode45(@(t, x2) v*cos((omega_max*T/2)/2 - (T*omega_max*sin((2*pi*T/2)/T))/(4*pi) + omega_max*(t-T1)), t2, x1(end));
    [t, x3] = ode45(@(t, x3) v*cos(omega_max*(T2-T1) + (omega_max*(t-T2+T1))/2 - (T*omega_max*sin((2*pi*(t-T2+T1))/T))/(4*pi)), t3, x2(end));
    [t, y1] = ode45(@(t, y1) v*sin((omega_max*t)/2 - (T*omega_max*sin((2*pi*t)/T))/(4*pi)), t1, 0);
    [t, y2] = ode45(@(t, y2) v*sin((omega_max*T/2)/2 - (T*omega_max*sin((2*pi*T/2)/T))/(4*pi) + omega_max*(t-T1)), t2, y1(end));
    [t, y3] = ode45(@(t, y3) v*sin(omega_max*(T2-T1) + (omega_max*(t-T2+T1))/2 - (T*omega_max*sin((2*pi*(t-T2+T1))/T))/(4*pi)), t3, y2(end));
    subplot(6, 1, [3 6]); hold off;
    plot(x1, y1, '.', 'MarkerSize', 12); hold on; grid on;
    plot(x2, y2, '.', 'MarkerSize', 12); hold on; grid on;
    plot(x3, y3, '.', 'MarkerSize', 12); hold on; grid on;

    % 出力データを生成
    pos = [x1, y1, theta1'; x2(2:end), y2(2:end), theta2(2:end)'; x3(2:end), y3(2:end), theta3(2:end)'];
    pos = [pos; x3_end, y3_end, omega_max*(T2-T1) + (omega_max*(T3-T2+T1))/2 - (T*omega_max*sin((2*pi*(T3-T2+T1))/T))/(4*pi)];
end

%% 出力情報
format long;
% 並進速度
velocity = v;
% 求めた軌跡の配列の長さ
length = size(pos, 1);
% カーブ終了から終点位置までの直線部分の長さを算出
extra_straight = max([(pos_target(2)-pos(end, 2)) / sin(pos_target(3)),(pos_target(1)-pos(end, 1)) / cos(pos_target(3))]);

%% 上で生成したグラフ(カーブのみ)を装飾
subplot(6,1,1);
title(sprintf('$$ \\dot{\\omega}_{max}: %.0f\\pi,\\ \\omega_{max}: %.0f\\pi $$', omega_dot/pi, omega_max/pi), 'Interpreter','latex', 'FontSize', 12);
xlabel('t', 'Interpreter','latex', 'FontSize', 12);
ylabel('\omega', 'FontSize', 12);
xlim([0, dt*length]);
subplot(6,1,2);
title(sprintf('$$ \\theta_{end}: %.2f\\pi $$', pos_target(3)/pi), 'Interpreter','latex', 'FontSize', 12);
xlabel('t', 'Interpreter','latex', 'FontSize', 12);
ylabel('\theta', 'FontSize', 12);
xlim([0, dt*length]);
subplot(6,1,[3 6]);
title(sprintf('$$ v_{max}: %.3f $$', v), 'Interpreter','latex', 'FontSize', 12);
xlabel('x', 'Interpreter','latex', 'FontSize', 12);
ylabel('y', 'Interpreter','latex', 'FontSize', 12);
axis equal;
xlim([min(pos(:,1)), max(pos(:,1))]);
ylim([min(pos(:,2)), max(pos(:,2))]);

%% スタート位置と直線部分を加味してプロット
pos_disp = pos_start + Rot_start * [adv_straight; 0; 0]+ Rot_start * pos';
figure(); hold on;
plot([0 pos_disp(1,1)], [0, pos_disp(2,1)], 'LineWidth', 4);
plot(pos_disp(1,:), pos_disp(2,:), 'LineWidth', 4);
plot([pos_disp(1,end), pos_disp(1,end)+extra_straight*cos(pos_end(3))], [pos_disp(2,end), pos_disp(2,end)+extra_straight*sin(pos_end(3))], 'LineWidth', 4);
axis equal;
xlim([round(min(pos_disp(1,:))/seg_half)*seg_half, ceil(max(pos_disp(1,:)-1)/seg_half)*seg_half]);
ylim([round(min(pos_disp(2,:))/seg_half)*seg_half, ceil(max(pos_disp(2,:)-1)/seg_half)*seg_half]);
xticks(-5*seg_half:seg_half/6:5*seg_half);
yticks(-5*seg_half:seg_half/6:5*seg_half);
grid on;

%% 情報の出力
% x[mm], y[mm], theta[rad]のCSV形式で保存
dlmwrite('data.csv', pos, 'precision', '%.10f');
dlmwrite('disp_data.csv', pos_disp', 'precision', '%.10f');
length
velocity
extra_straight

出力はこんな感じになります.
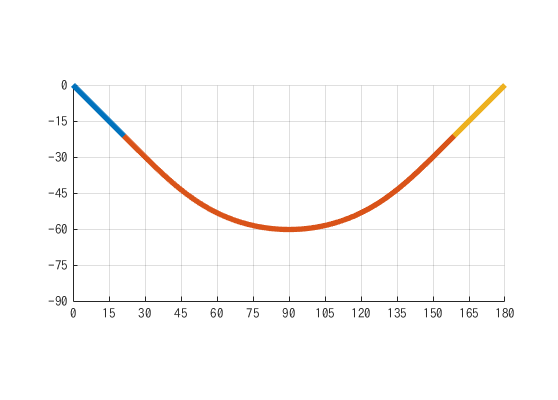
trjExp

そしてこれをマイクロマウスの最短走行に使われる全ての軌道について生成しました.
種類としては, 大回り90度ターン, V90, 135度ターン, 180度ターンについてそれぞれ生成しています.
スクリプトの最後でdlmwrite関数を使って1mm間隔で$x,y,\theta$の点列データを作成します.

マイコンでの実装 

先程得られた点列の$x,y,\theta$のデータをMATLABでファイルに書き込んだものをコピーしてきて, 構造体の初期化をするところに直接突っ込みます.
構造体に入れやすいようにデータをファイルに書き込む, いっそCコードをMATLABから生成するのがおすすめです.
ここから, 実際にプログラムを書きていきます. 制御周期を1ms, 追いかける軌道を5msで更新します.
方針としてはわりかし単純で

  1. まず, 軌道追従の最初の点を目標の点として現在の自己位置との誤差を計算し, (3)式に代入してモーターへの入力を与える.
  2. 5msごとに5msの間の並進方向の速度の積分をとって, 次の目標点を考える.
    例えば, 5msの間1000mm/sで動いてたなら, $1000m/s * 0.005s = 5mm$より, 前回の目標点より5つ先の点列を目標点として与える.(軌道は1mm間隔でとってるの5つ先)
  3. 次の目標点と自己位置との誤差を計算して, また(3)式に代入する.
  4. 2.3.を繰り返す.
    イメージとしてはマリオカートで眼の前にいる最速タイムを出しているゴーストを追いかけているという感じです.
    以下がイメージ図です.(右下は雅号です. 気にしないでください)
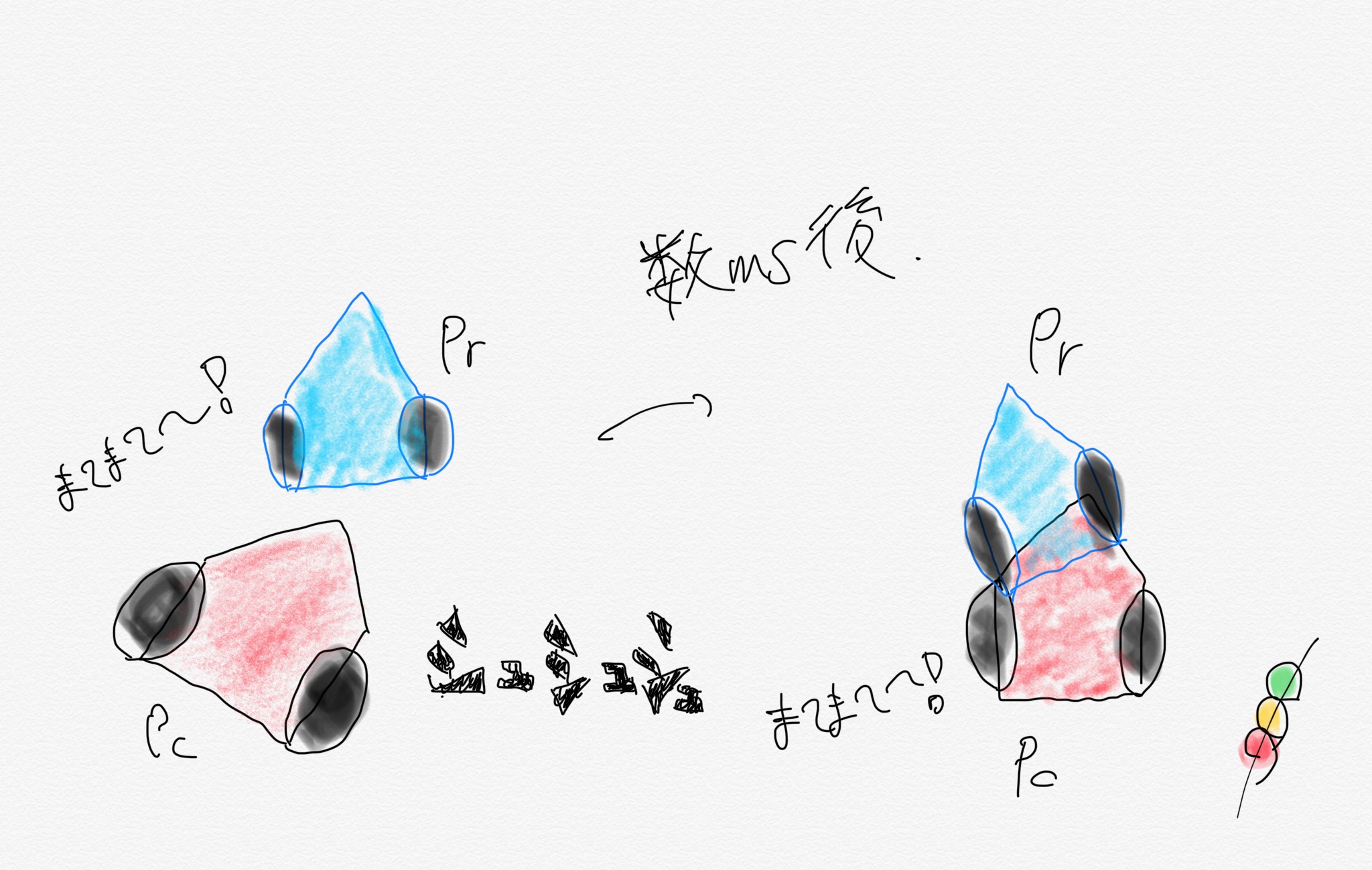
    chasingImage

実装としてはこんな感じです.(変数が宣言されてなかったりしてますが, 方針を示しているだけなので気にしないで下さい)
ただし, 私の座標系はこのようになってるので, 速度コントローラへの入力($e_x$)につく符号が違ったりしています.

myCoordinate

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

while(1){
  if(ENCODER_start == ON){ //1msの割り込み
    read_encoder();  //エンコーダの値を読む
    robot.add_coordinate(degree); //自己位置の更新
    speed_controller(now_velocity * cos(theta_e) + Ky * e_y, w_r + now_velocity * (-Kx * e_x + Ktheta * sin(theta_e))); //Kanayama Control Method
    ENCODER_start = OFF;
  }
  if(traject_clock == ON){//5msの割り込み
    traject_clock = OFF; 
    uint16_t dst_len = now_velocity * 5.0 / 1000.0; //次は何個目の点列を見るか計算
    target_index = (target_index + dst_len) % index_size; // 点列更新

    dotData ref = traject.get_data(target_index, Operation::TURN_RIGHT90, NORTH); //target_index個目の点列データを取得.
    e_x = ref.x - robot.x();      
    e_y = ref.y - robot.y();
    float tmp = e_x; //偏差をロボット座標系に変換
    e_x = tmp * cos(degree / 180.0 * PI) + e_y * sin(degree / 180.0 * PI);
    e_y = -tmp * sin(degree / 180.0 * PI) + e_y * cos(degree / 180.0 * PI);

    w_r = (ref.rad - (traject.get_data((target_index - dst_len) % index_size, Operation::TURN_RIGHT90, NORTH).rad)) * 200.0; //thetaの差分からw_rを計算
    theta_e = ref.rad - degree / 180.0 * PI;
    if(last_index > target_index) flag = true; //点列が一巡したら終了
    else last_index = target_index;
  }
}

ロボットのソースコードはGitHubにあげているので参考にしてみてください.
src/mazesolver.cpp辺りです.
Dangoromouse

するとこんな感じに走ります.
走っているロボットはシステム同定をした際のロボットです. 詳細はこちら.
NigLacerto

マイコン内部のデータをプロットした結果, このようになりました. オレンジが目標軌道, 水色と黄色が自己位置です.
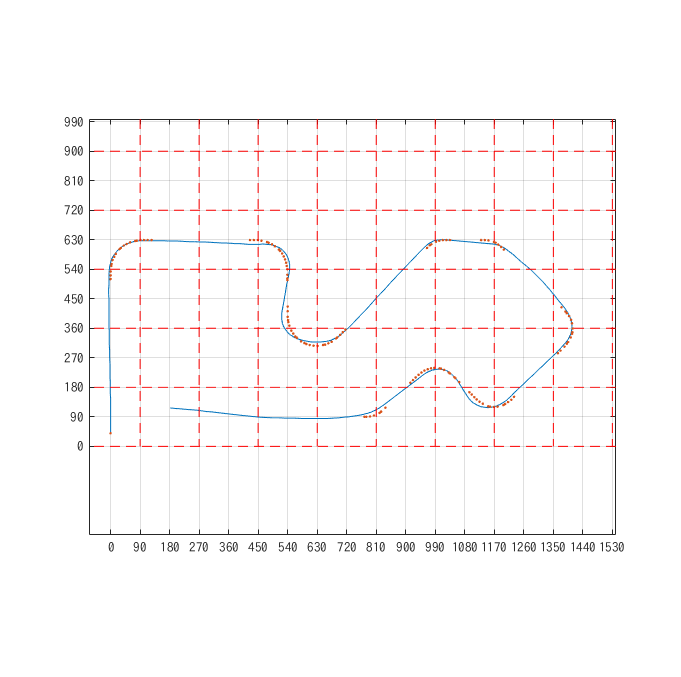
chaseLog

以下, 軌道追従をした所感です.

所感 

走行がセンサーに対して敏感になる. 

自己位置を推定してそれに頼って走ることになるので, 壁にぶつかる, タイヤが空転すると自己位置がおかしくなり, 即座に走れなくなります.
外界センサーを使って位置を直すにしてもやはりそれでもセンサーに対して敏感になってしまいます.

高速化するとスリップ角を無視できなくなる. 

上述のツイートでも書いてますが, スリップ角が生じるとそもそも, 自己位置を正しく取れなくなります.
自己位置の推定にスリップ角の概念を導入しないと全く別の場所を走ったりするようになってしまうので注意です.

ロボットが突然速くなるわけではない 

上述の理由より, 軌道追従をしたからといってマウスが速くなるわけではないです.
正確に, そして速く走るためにも自己位置を正確に推定することが大切のように思えます.

ターンの終わりなどで振動する & パラーメータの選定がよく分からない. 

Kanayama Control Method は上で見たとおり, 実装はとても簡単なものになりますが, 論文内でも漸近安定までしか証明できてないせいか. 軌道に追従するものの, 遅かったり, 振動してしまうように感じます.

今の私の実装では, (3)の式の角速度の項に位相補償するものを付け加えてほんの少し改善したかと思います.
ただ, 私が正しく(3)式に出てくるパラメータを選べなかった, そもそもハードの作りが甘かった等の問題があるので, 今後も調べていきます.

しかし, マイクロマウスの競技上, 速度をかなり上げて走らせてるので, ロボットがターンするときに1G以上かかるみたいな事がない分には十分に追従していくと思います.

まとめ 

軌道追従はこんな感じになります. 色々と改善点はありますが, 軌道追従の一番の魅力は軌道さえ生成できればその通りに走る事と再現性のある走りができる事じゃないんかなと思います.(ロボトレースとかでやるとすごく面白そうですが, 私はロボトレースをやる気運はないので誰か頼む)

今後はこちらのブログで紹介されている線形化フィードバックを作った後に, 軌道追従コントローラーを作って軌道追従をさせたいかなと思いました.
独立二輪車型ロボットで目標軌道に追従する制御をする②

最後に元気に軌道追従で走る私のマウスの動画を貼って終わりにしたいと思います.