初めに 

Q: マイクロマウス2019はどうでしたか？
A: 記憶がない. 来年がんばりゅ

こちら, Micro Mouse Advelent Calendar 2019 28日目の記事です. 嘘です. 昨日の記事はないですし, 明日の記事もないです.

そうなんだよな. 昨日も明日もそんな概念はなくて, ただ今日という日が連綿と続いていくだけなんだよな.
将来を考えて云々とか体のいい言葉はあるけど, 今日という日を大切にしないで生きてきた結果, 日々の連続の先にあるその未来で存在しないはずの夏の幻覚に囚われている. 多分この先もそうなんだろう.

その点, 冬は寒くて生存競争が激しいので一日生きられただけで自己肯定ができる. 冬はすごい. 違うこういう話じゃない. いや, したいけど今ここで書くべきではない. 四季が移り変わっていくのって百合なんだよな.

概要 

マイクロマウス競技(ここでは主に旧ハーフサイズの)では小さなロボットの機体の中に様々な機能を詰め込む必要があります. その中でも難しいのが速度を推定するためのエンコーダーです.
というのも, これは1マス90mm×90mmの迷路の中を走るロボットに使えるエンコーダー付きモーターがあまり存在しない＆あっても1個n万なので学生の財布が死んでしまう という問題点があるからです.

これを解決するために, マイクロマウスに参加する多くの競技者は回転するモーターの軸に磁石を取付け, ロボットの基板(ここではバッテリーなどを載せている底の基板) に基板を垂直方向に立て, そこにAngle sensorをつけて磁石の回転から速度を推定するといった感じでエンコーダーを自作します. (なんで基板が構造材になって走ってるんだろうね. 不思議だね.)

しかし, 使える磁石のサイズが車体の大きさによって制限されたり, そもそも工作精度(磁石とエンコーダの位置にズレがある等)に限界があるので, 往々にして得られる信号はノイズだらけです.
こちらの「ロボットにステップ応答を入れた後に初めてエンコーダの信号を見て絶望する人間」をご覧ください.

このように

  • 磁石をエンコーダーの真上に配置できないがために生じる周期性ノイズ
  • 小さい迷路を走る都合上, データシートギリギリ(なんなら下回ってる)のサイズの磁石を使わないといけないハードウェアの制約
  • モーターの磁力などに由来するその他非線形ノイズ
    の影響でエンコーダーのSN比が否応なしに劣化していきます.

これの対策として

  • 頑張って大きい磁石を使えるようにハードウェアを設計する
  • エンコーダーの垂直方向に磁石の中心が来るように調整する
    • 多分これが一番やりやすいやつです. ちなみに筆者はずれているのを直すのがめんどくさい(基板を発注する時間と元気がない)ので, サボってます.(おい)
  • エンコーダ付きモーターを買う
    などが考えられますが, モーターを買う以外の選択肢を選んだ場合でも非線形ノイズなどは乗ってしまいます.

そこで本記事ではソフトウェア的に処理する方法について書いていきます.

本文 

移動平均フィルター 

得られた信号のノイズの影響を抑える手法として一番最初に思いつくのは移動平均フィルターではないでしょうか. 実際, マイクロマウスに取り組んでいる人達もこのフィルターを使っています.
移動平均フィルターは過去数回分のデータを取り, その平均を求める処理です. 時刻 $t$ におけるエンコーダの値を $v_{enc}(t)$ ,推定値を $v(t)$ とすると,
移動平均フィルターは
\begin{equation}
v(t) =\frac{1}{N}\sum ^{N-1}{n=0} v{enc}( t-n)
\label{show-sma}
\end{equation}

Eq.$\eqref{show-sma}$ についてz変換を行うと
\begin{equation}
V(z) =V_{enc}( z)\frac{1}{N}\sum ^{N-1}{n=0} z^{-n}
\end{equation}
となります. これより, 移動平均フィルターの伝達関数 $H{MA}(z)$は以下のように表せます.

\begin{eqnarray}
H_{MA}(z) =\frac{V( z)}{V_{enc}( z)} &=&\frac{1}{N}\sum ^{N-1}_{n=0} z^{-n}\\\
&=&\frac{1}{N}\frac{1-z^{n}}{1-z^{-1}}
\end{eqnarray}

これを用いてモーターにステップ入力を加えたときの速度推定を行うと, 以下の図のような結果が得られます. 今回は $N=10$で取りました.

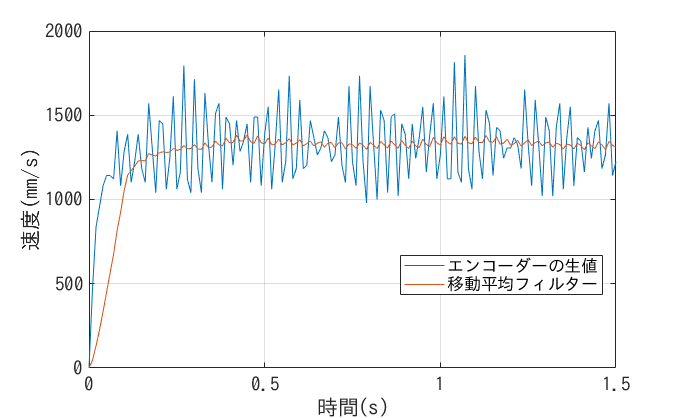
Images

定常応答こそ改善されましたが, 過渡応答はずいぶん遅れてしまいました. 終わり.

ローパスフィルター 

そもそも, 移動平均フィルターの最大の問題点はカットオフ周波数の設計ができない(位相が不連続)(これを正しく表現できる言葉ってなんでしょう？)ということです.
移動平均フィルターの周波数応答をプロットしてみると, 以下のようになります.
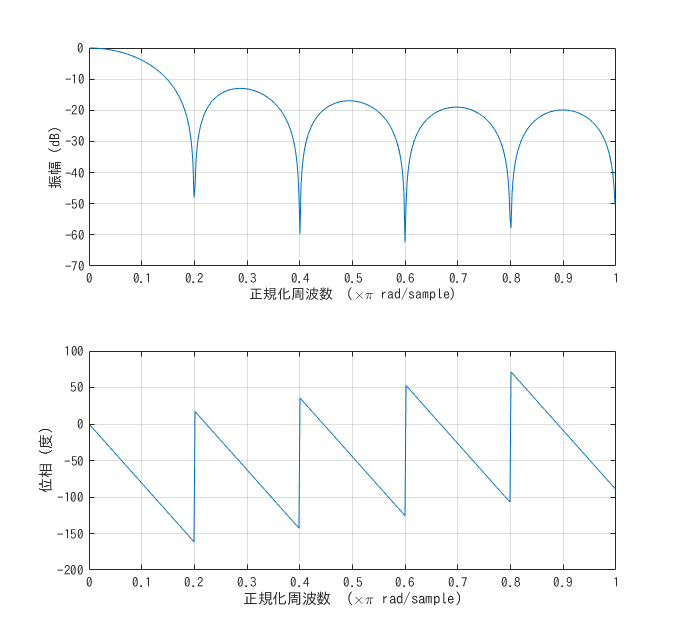
Images

マイクロマウスの競技者に話を聞くと複数の移動平均フィルターを組み合わせて速度を推定していたりしますが, このように位相が不連続になるので, 速度計画によっては速度の推定自体がうまくいかないという問題点があります.

それを回避するため, カットオフ周波数などを設計できるようにローパスフィルターを使った実装が考えられます.

ローパスフィルターは連続時間では以下のように記述されます. ここで$\tau$は時定数です.
$$
Y( s) =\frac{1}{1+\tau s} X(s)
$$
これに対して, 後退差分

\begin{equation}
s=\frac{1-z^{-1}}{T}
\end{equation}
を施して離散化すると

\begin{eqnarray}
Y( z) &=&\frac{1}{1+\tau \frac{1-z^{-1}}{T}} X( z)\\\
&=&\frac{T}{T+\tau \left( 1-z^{-1}\right)} X( z)
\end{eqnarray}

となります. ここで$T$はサンプリング周期です.

これに対して, 逆z変換すると, ローパスフィルターはこのような形になります.
\begin{eqnarray}
( T+\tau ) y( k) -\tau y( k-1) =Tx( k)\\\
( T+\tau ) y( k) =\tau y( k-1) +Tx( k)\\\
y( k) =\frac{\tau }{T+\tau } y( k-1) +\frac{T}{T+\tau } x( k)
\end{eqnarray}
ここで, $\alpha = \frac{\tau}{T+\tau}$とおくと, ローパスフィルターは以下の形に変形できます.
\begin{equation}
y(k)= \alpha y(k-1) + (1-\alpha) x(k)
\end{equation}
ここでカットオフ周波数$F_c$は
\begin{equation}
\tau = \frac{1}{2 \pi F_c}
\label{cutoff}
\end{equation}
となります.
ここらへんの処理についてはモーター制御マンさんのQiitaの記事(最も簡単な「一次のローパスフィルター」を作る方法)に詳しく書いてあるのでこちらも見てみてください.

これで, カットオフ周波数などを設計できるようになりましたが, 位相が遅れることには変わりがないので, このままでは速度推定は不十分です. この問題に対処するために加速度センサーとエンコーダーを組み合わせた相補フィルターを次に紹介します.

相補フィルター 

そもそも, エンコーダーは時間あたりのパルス数から時間微分という操作を行って一秒あたりの速度を計算しています. この微分という操作が信号の高周波成分を影響を増大させてしまいます.

また, 加速度センサーを用いて得られた加速度を積分して速度を計算するという方法も考えられますが, この積分という操作は信号の低周波数成分を増大させるので, ドリフトなどの定常偏差が計測データに乗ってしまうと, 時間が経つにつれて推定した値がずれていってしまいます.

そこで, 高周波数成分のノイズが乗ってしまうエンコーダーから得られるデータにローパスフィルターをかけ, ドリフトなどの低周波数成分のノイズが乗ってしまう加速度センサーから得られたデータにハイパスフィルターをかけるといい感じにノイズが除去できそうです！

ここで加速度によって得られる速度を$v_{acc}(z)$, エンコーダーから得られる速度を$v_{enc}(k)$, 速度の推定値を$v(k)$とすると相補フィルターは以下のように表現できます.

\begin{equation}
V( z) =H_{high}( z) V_{acc}( z) +H_{low}( z) V_{enc}( z)
\label{proposed}
\end{equation}

ここで, $H_{low}(z)$, $H_{high}(z)$はそれぞれローパスフィルターとハイパスフィルターで, 連続時間のフィルター
\begin{equation}
H_{low}( s) =\frac{1}{1+\tau s} ,H_{high}( s) =\frac{\tau s}{1+\tau s}
\end{equation}
に対して, 後退差分を取ったものになります.

\begin{equation}
H_{low}( z) =\frac{T}{T+\tau \left( 1-z^{-1}\right)} ,H_{high}( z) =\frac{\tau \left( 1-z^{-1}\right)}{T+\tau \left( 1-z^{-1}\right)}
\end{equation}
これらの周波数特性について見てみると

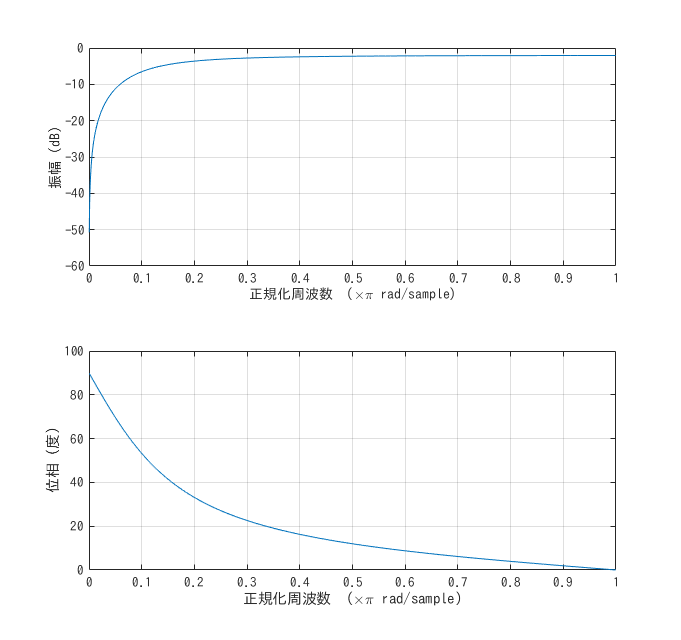
ハイパスフィルターの周波数特性

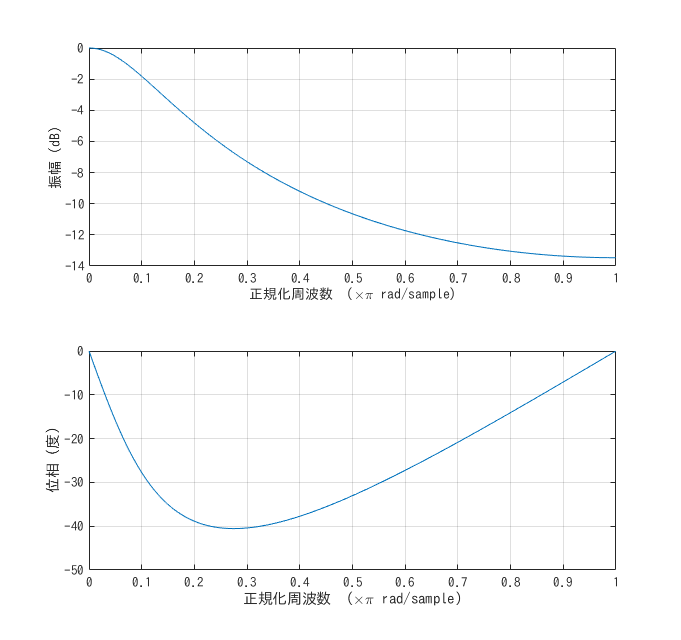
ローパスフィルターの周波数特性


ちゃんと相補的になっています.

Eq.\eqref{proposed}を変形していくと,
\begin{equation}
V( z) =\frac{\tau \left( 1-z^{-1}\right)}{T+\tau \left( 1-z^{-1}\right)} V_{acc}( z) +\frac{T}{T+\tau \left( 1-z^{-1}\right)} V_{enc}( z)
\label{proposed2}
\end{equation}
ここで, 加速度$a(k)$と加速度によって求まる速度$v_{acc}(k)$の関係は
\begin{equation}
v_{acc}( k) =v_{acc}( k-1) +Ta( k)
\end{equation}
なので, これに対してz変換すると

\begin{eqnarray}
V_{acc}( z) &=&z^{-1} V_{acc}( z) +TA( z)\\\
\left( 1-z^{-1}\right) V_{acc}( z) &=&TA( z)\\\
\therefore \frac{V_{acc}( z)}{A( z)} &=&\frac{T}{1-z^{-1}}
\end{eqnarray}
となります. よって離散積分は$\frac{T}{1-z^{-1}}$と表現できます. これをEq.\eqref{proposed2}に代入すると
\begin{eqnarray}
V( z) &=&\frac{\tau \left( 1-z^{-1}\right)}{T+\tau \left( 1-z^{-1}\right)}\frac{T}{1-z^{-1}} A( z) +\frac{T}{T+\tau \left( 1-z^{-1}\right)} V_{enc}( z)\\\
\left( T+\tau \left( 1-z^{-1}\right)\right) V( z) &=&\tau TA( z) +TV_{enc}( z)
\end{eqnarray}

これに対して, 逆z変換 すると最終的な形が求まります.

\begin{eqnarray}
( T+\tau ) v( k) -\tau v( k-1) &=&\tau Ta( k) +Tv_{enc}( k)\\\
v( k) &=&\frac{\tau }{T+\tau }( v( k-1) +Ta( k)) +\frac{T}{T+\tau } v_{enc}( k)\\\
\therefore v( k) &=&\alpha ( v( k-1) +Ta( k)) +( 1-\alpha ) v_{enc}( k)
\end{eqnarray}

とても単純な形になりました！ここで$\alpha$とカットオフ周波数$F_c$の関係はEq.$\eqref{cutoff}$から
\begin{equation}
\frac{1}{1+2\pi T F_c} = \alpha
\end{equation}
となります.

実装 

実装はこんな感じになります. そのまんまですね.

最後に相補フィルターを使って速度推定をしてみました.
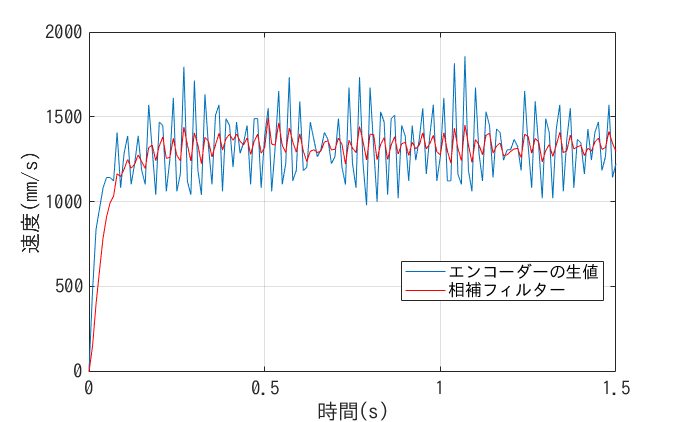
Images
移動平均フィルターを使ったときに問題になった過渡応答の時の推定の遅れがずいぶん解消されました. 定常応答の時に推定値が震えているのは実機の実験をフローリングの床(周期的に段差があってホコリが多い…)でやった影響で加速度センサーに想定してない外乱が増えたためだと思います.
実際の迷路で走らせたらもう少し良くなるはず.

Future Work 

このブログを書いた人がマウスを走らせられる状態になくて未検証な事がいくつかあるので, Future Workとしてメモします.

実際の走行での評価 

テストしたケースがステップ応答を見たこれ一つだけなので, 他のパラメータ(具体的にはマイクロマウスが最短走行する際のパラメータで正しく推定できるか)を検証していく.

$\alpha$(カットオフ周波数)の設計 

これがなーんも分からん.
エンコーダの軸位置のズレによる周期ノイズは周期がエンコーダの回転数に依存することは分かるんですが, 非線形ノイズとかそもそものエンコーダとジャイロセンサーのモデルが分からん！ｗという感じなので, ここはよく分からないです.
今回は$\alpha = 0.65$ぐらいで実装しているのですが, どうなんでしょうか.

オブザーバーの実装 

今の実装では路面状況によって加速度センサーにスパイクノイズが入ったり, タイヤが滑ったりすると正しく速度推定ができないので, これに対処するためにオブザーバーを実装して速度推定できないかなと思ってます.
ロボットのモデル自体はシステム同定で求めたので, それを使っていきたいですね.
簡単なシステム同定については昔, こちらの方に書いたのでどうぞ興味のある方は見てみてください.
MATLABでマイクロマウスの機体をシステム同定してPIDチューニングする.

まとめ 

対向二輪車の速度推定に相補フィルターを使うことで, ノイズに対して頑健な速度推定ができるようになりました. 今後は実際に迷路で最短走行を走らせた時の推定の様子を見たり, オブザーバーの実装などをしていきたいですね.

P.S. 

そういえば, 技術書典8に出ることになりました. CMSIS-DSPについて書いていくので, 良かったら買っていってね.